Marta Vela
La proporción áurea es un fenómeno que parte de la propia naturaleza y que, representado por una ecuación algebraica, se muestra como un segmento dividido en dos partes desiguales cuyo punto de encuentro radica en el número 1,618. El segmento grande se denomina con la letra griega phi y el pequeño, con la letra griega psi; en porcentaje, ambas partes se pueden calcular como un 62% y un 38%, respectivamente. En la música anterior a 1900, ¿existe la proporción áurea? ¿su uso era deliberado, como en el siglo XX?

La proporción áurea es un fenómeno que parte de la propia naturaleza y que, representado por una ecuación algebraica, se muestra como un segmento dividido en dos partes desiguales cuyo punto de encuentro radica en el número 1,618.
El segmento grande se denomina con la letra griega phi–en honor al escultor griego Fidias–y el pequeño, con la letra griega psi; en porcentaje, ambas partes se pueden calcular como un 62% y un 38%, respectivamente.

Figura 1: proporción áurea y porcentajes
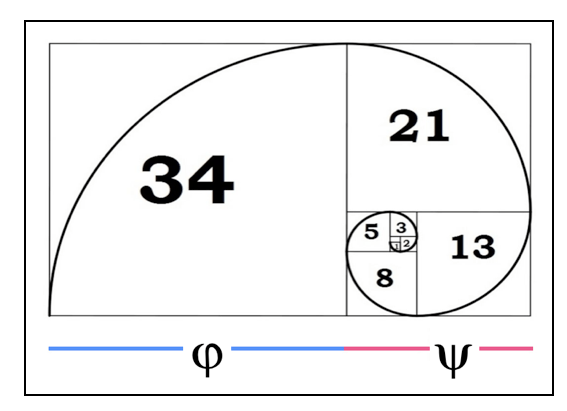
Los griegos adoptaron la proporción áurea como paradigma de belleza en el arte y en la naturaleza, y el número irracional 1,618 se convirtió en el número divino–y también dorado. A la proporción áurea se añade la famosa serie de Fibonacci –aquélla en que la suma de dos números consecutivos resulta el siguiente de la sucesión– íntimamente relacionada, como veremos, con el número dorado: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc. Si dividimos cada número entre el precedente, el valor resultante se acerca, excepto en los dos primeros casos, a 1,618; si dividimos cada número con el siguiente, el valor está en torno a 0,618:
1/1 = 1
2/1 = 2
3/2 = 1,5
5/3 = 1,666
13/8 = 1,625
21/13 = 1,615
34/21 = 1,619
55/34 = 1,617
89/55 = 1,617
1/1 = 1
1/2 = 0,5
2/3 = 0,666
3/5 = 0,6
8/13 = 0,615
13/21 = 0,619
21/34 = 0,617
43/55 = 0,618
55/89 = 0,617
La representación de los primeros números de la serie sobre la superficie de un folio apaisado en distintas subdivisiones geométricas muestra la relación entre la proporción áurea y la serie de Fibonacci, con una espiral que une todas las partes entre sí de un solo trazo:
Figura 2: proporción áurea y serie de Fibonacci
Por tanto, la proporción áurea ha tenido una gran influencia sobre las artes plásticas hasta la actualidad…
Figura 3: La Gioconda, Las meninas y el Partenón
… y también sobre la música.
La proporción áurea fue uno de los recursos estructurales más utilizados por los compositores del siglo XX: generalmente, los compositores utilizaron la sección áurea para estructurar las secciones de las obras o bien para establecer un punto culminante justo en la intersección de los dos segmentos.
Para Debussy, la serie de Fibonacci era un asidero tan importante como lo había sido la forma sonata en los dos siglos precedentes y rara es la obra, entre su ingente repertorio orquestal, pianístico, vocal o de cámara, en la que no haya resonancias áureas en la forma. Se puede encontrar muchos ejemplos en toda su música, como los 55 compases de introducción del tercer movimiento de La Mer, Dialogue du vent et la mer; los 21 compases de introducción en Ronde de Printemps en las Images pour orchestre; los 34 compases del 3/8 de Jeux; los 34 compases de progresión previos a la coda en L’ isle joyeuse, como en la recapitulación de Masques, los 55 compases en el clímax de Reflects dans l’ eau, todos estos ejemplos están formados conforme a una estructuración consciente, a partir del número divino, tal y como Debussy expresa en esta carta a su editor, Durand, a propósito de la publicación de Estampes en 1903:
You’ll see, on page 8 of Jardins sous la pluie, that there are a bar missing, my mistake, besides, as it’s not in the manuscript. However, it’s necessary, as regards number, the divine number, as Plato and Mlle Liane de Pougy would say, each admiratedly for different reasons (Howat, 1989:6).
Bartók fue un paso más allá, dado que la proporción áurea no sólo estructura la forma de la obra, sino que determina el devenir armónico de la música y los intervalos que conforman los acordes:
Calculado en semitonos: 2 representa una segunda mayor, 3 representa una tercera menor, 5 representa una cuarta justa, 8 representa una sexta menor, 13 representa una octava aumentada. El tejido musical puede imaginarse como construido exclusivamente con células de 2, 3, 5, 8 y 13, en tamaño, con sus divisiones que siguen las proporciones dadas por la serie arriba indicada. Así, el 8 puede dividirse solo en 5 + 3 (Lendvai, 2003:45).
Ahora bien, en la música anterior a 1900, ¿existe la proporción áurea? ¿cómo podemos hallarla? ¿su uso era deliberado, como en el siglo XX?
Sin duda, durante el siglo XX, ante la paulatina desaparición de las formas musicales del pasado –fundamentalmente, la forma sonata y la fuga– los compositores tuvieron necesidad de encontrar otro método de estructuración formal de la música y recurrieron a la sección áurea, una estrategia que dura hasta la actualidad.
Pero, incluso, en las formas tradicionales, podemos ver vestigios de la sección áurea: la herramienta más fiable consiste en multiplicar el número total de compases por 0,618–siempre que el compás sea el mismo durante toda la obra–y el valor resultante se convierte en el punto de unión entre las dos partes, la sección áurea (S.A.). Posteriormente, en sucesivas multiplicaciones, se pueden ir obteniendo nuevas particiones, como ocurre en el caso de los ejemplos anteriores.
Estudiemos la Fuga n º 11 del primer volumen del Clave Bien Temperado, de Johann Sebastian Bach. Si multiplicamos el número total de compases, 72, por 0,618, resulta un punto estructuralmente importante, justo marca el final de segundo estrecho–sección donde el tema principal aparece sucesivamente en todas las voces–y prepara la resolución de la cadencia sobre Re menor, relativo de la principal. En sucesivas subdivisiones, si multiplicamos 44,49 por 0,618 sale 27,49, que se corresponde con el primer estrecho, y, más concretamente, con la entrada de la voz superior; si multiplicamos de nuevo 27,49 por 0,618, marca el fin del contrasujeto y la llegada a Do mayor, la dominante de la tonalidad principal, Fa mayor.
Figura 4: J. S. Bach: Fuga XI, CBT I
Podemos encontrar un nuevo ejemplo en la Sonata Hob. XVI: 34 en Mi menor de Haydn, en el primer movimiento. Sobre un número total de compases de 127, con la consabida multiplicación por el número áureo, obtenemos un valor de 78,48, justo el último compás del Desarrollo, que da paso a la Recapitulación de la sonata. En sucesivas multiplicaciones podemos ver otros puntos interesantes de la forma sonata, a saber, el primer tema del Desarrollo, la Segunda Sección y la Transición o puente.
Figura 5: J. Haydn: Sonata n º 53, I
En las obras anteriores, ¿es deliberado el uso de la sección áurea? En realidad, nunca lo sabremos con certeza, pero, dado que la música no puede diseñarse con escuadra y cartabón–como un lienzo o un templo–la utilización de las proporciones áureas puede tener un componente intuitivo, fruto del contexto artístico en que los compositores se educaron, al igual que otros parámetros musicales, como la forma musical o los preceptos de la armonía.
El sistema se aprendía del mismo modo que los niños aprenden un idioma, es decir, escuchando a sus padres y a sus hermanos mayores y a amigos, no estudiando la gramática y sintaxis (Rosen, 2010: 22).
La armonía, tal y como se enseña en nuestros tiempos en las escuelas, impone reglas que no fueron fijadas sino mucho tiempo después de la publicación de las obras de las que han podido ser deducidas, pero que sus autores ignoraban. Nuestros tratados de armonía basan así sus referencias en Mozart y en Haydn, quienes jamás oyeron hablar de tratados de armonía (Stravinsky, 2006: 42).
Desde aquí os animo a que reparéis en cosas tan cotidianas como un folio Din A4, una tarjeta de crédito o el interfaz de Twitter y, por supuesto, tirando de calculadora –quien lo pueda a hacer de cabeza, magnífico–, os animo también a investigar los secretos áureos que sin ninguna duda esconde el repertorio de cualquier músico.
Bibliografía básica
CORBALÁN, F., (2010): La proporción áurea, el lenguaje matemático de la belleza, Barcelona, RBA.
HOWAT R., (1989): Debussy in proportion: a musical analysis, New York, Cambridge University Press.
LENDVAI, E., (2003): Béla Bartók: un análisis de su música, Cornellà de Llobregat, Idea Books.
ROSEN, C., (2010): Música y sentimiento, Madrid, Alianza, 22.
STRAVINSKY, I., (2006): Poética musical, Barcelona, Acantilado.